To investigate simple gas laws and explain them in terms of kinetic molecular theory.
As you may recall from your discussion of the scientific method, a scientific law is a summary of experimental results and does not provide an explanation.
In this experiment, we will explore some of the gas laws that empirically describe the behavior of ideal gases and attempt to explain these using the kinetic molecular theory of gases.
While gas molecules vary in their molecular geometry and polarity, many gases behave in a similar manner. The macroscopic behavior of most common gases at room temperature can be described to a very good approximation by the simple gas laws:
A gas that obeys these gas laws is defined as an ideal gas. While no gas obeys the ideal gas law exactly, most gases at room temperature and pressure do follow the ideal gas law to a large extent.
When put together, the overall set of properties of an ideal gas can be summarized by the ideal gas law:
(6)
where the pressure is reported in atmospheres, the volume is in liters, is the number of moles of gas, is in Kelvins, and the ideal gas constant . [1]
In this experiment, we will study the extent to which Boyle’s Law and Charles’ Law can describe the behavior of a gas and attempt to use this to determine the number of moles of gas present.
It has been postulated based on the particulate nature of matter that an ideal gas can be described using the kinetic molecular theory. Here are the postulates of this theory: [2] In this model, a gas is modeled as a collection of particles in constant motion, which move in a straight line until a collision occurs. [3]
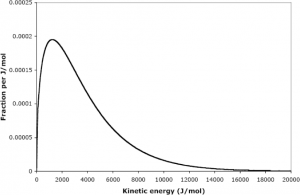
It is important to recognize here that it is the average kinetic energy, not velocity (recalling from physics that the kinetic energy is ), that is proportional to the temperature. Furthermore, the energies of different particles form a distinct distribution as illustrated below:

In this model, we recognize that gas pressure arises due to the force associated with the collision between particles of a gas and its container. Furthermore, we can show that, using classical physics, we can use the kinetic molecular theory of gases to back-derive the ideal gas law. [4]
In this experiment, we will not attempt to quantitatively derive the gas laws from kinetic molecular theory; rather, we will try and visualize what happens at the particulate level and apply the kinetic theory of gases and develop explanations this way.
In this experiment, you will use the PhET Gas Properties simulation to examine Boyle’s Law, and attempt to visualize how this can be explained using the kinetic molecular theory of gases.
In this case, we wish to plot (a) as a function of box width (a measure of volume), and (b) 1/(number of collisions) as a function of box width. In making these plots, you must incorporate appropriate measures of uncertainty, which we can roughly specify as a standard deviation. These are then incorporated in as error bars, as shown on the following example plot:
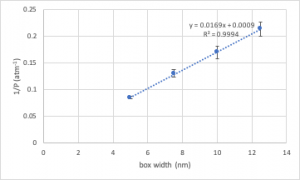
To find the error of given the error in pressure, you need to find the fractional error in and then
This video demonstrates how you would create these plots using Microsoft Excel:
In this experiment, you will study the relationships between volume and temperature using Gary Bertrand’s Gas Properties simulation. Select the Charles’ Law tab and complete the following.